
Test it
Preliminary Version, to appear in Proceedings of ACM Web3D Symposium, Monterey,Feb. 2000
AbstractIn this paper we discuss the benefits of extending VRML by constraints and present a new way based on prototypes and scripting to implement this extension. Our approach is easy-to-use, extensible and it considerably increases the expressivity of VRML. Our implementation supports one-way equational and finite domain constraints. Finally we argue that in the long run constraints should become an integral part of VRML. |
EXTERNPROTO Constraint [
field MFString inames
field MFString innodes
field MFString protoField
field MFString protoType
field MFString domains
field MFString domainDefs
field MFString userFunctions
field SFBool startEval
field SFBool eventFirstPriority
field MFString constraints
]
"ProtoConstraint.wrl#Constraint"
Some of the fields of the Constraint prototype are only needed as work arounds
for missing functionality of the Java Scripting API. We need the inames and inodes
to bind nodes to names because there is no function getNode(DefName) in the JS API as we know it
from the EAI.
Furthermore the fields protoField and protoType map fields of a node,
which is an instance of a user defined prototype, to their types. This is necessary because we can not
get the type of a field via the JS API.
The fields domains and domainDefs are only used for finite domain constraints. In the domains-field the user assigns one of the domains defined in the domainDefs-field to the variables used in the constraints.
The field userFunctions offers the possibility to add any needed function to the constraint solver and use these functions in the constraints. The syntax needed to support this feature is very easy: First, the user has to define the signature of the function and then the function can be defined in JavaScript syntax. The signature consists of the return type, the function name and the parameter types.
The value of startEval determines whether the constraints will be solved
at initalization of the Constraint or not.
Furthermore, the value of eventFirstPriority controls whether values set
by an event can be changed by the constraint solver or not.
eventFirstPriority is TRUE by default. In this case, the
events from VRML scene graph have highest priority and will not be changed
by the solver. As an example consider, that you want to move an object in a
room using a PlaneSensor. If eventFirstPriority
is TRUE, no collision-handling possible. By collision-handling we
mean detection of a collision and automatically moving the object
to a non-colliding position. Without collision-handling the object
can move through walls or things standing in the room. Therefore, it is necessary
to set eventFirstPriority FALSE.
Now, if the objects approaches the wall, the constraint solver is able to prevent the collison.
Finally, the field constraints contains a list of strings (MFString),
each string represents a constraint. The constraints are interpreted as
one-way equational constraints if domains
and domainDefs are empty and as finite domain constraints, otherwise.
lights.on=or(switch1.on,switch2.on)In the above example the value of lights.on is updated whenever the value of switch1.on or switch2.on changes. One-way constraints have been used for many purposes including layout, animations and user-interfaces. They can express relations like attachment or noncollision of objects or enforce physical laws. Their success is mainly due to three factors: they are efficient, intelligible and domain-independant. Different algorithms for solving such constraints, even for dynamically changing sets of objects and constraints are described in [Zanden_et_al:94]. In this case constraints have to be activated or deactivated when objects are created or deleted.
Now, we want to show how to use one-way constraints in VMRL by means of examples.

With the help of constraints we want to enforce 3 restrictions:
The pieces cannot be moved from the board, the pieces are always
centered in a square on the chess board and when moving a piece it cannot
pass through another piece. The first 2 restrictions are realised
with the user-function CenterField. The third restrictiion
is achieved by lifting a piece before it is moved.
Constraint {
startEval TRUE
eventFirstPriority FALSE
userFunctions [
"SFFloat CenterField(SFFloat)"
"function CenterField(val) {
var help=Math.round(val);
if (help>7) help=7;
if (help<0) help=0;
return help;
}"
]
inames [ "PS1" "piece1" "PS2" "piece2" ]
inodes [ USE PS1, USE piece1, USE PS2, USE piece2 ]
constraints [
"piece1.translation[0]=CenterField (PS1.translation_changed[0])"
"piece1.translation[1]=If(PS1.isActive, 2, 0.5)"
"piece1.translation[2]=CenterField (*(-1, Ps1.translation_changed[1]))"
"piece2.translation[0]=CenterField (PS2.translation_changed[0])"
"piece2.translation[1]=If(PS2.isActive,2 , 0.5)"
"piece2.translation[2]=CenterField (*(-1, PS2.translation_changed[1]))"
]
}
Note, that the Y-coordinate
of the PlaneSensor, that controls the piece is assigned to its Z-coordinate
because the chess board lies in the X-Z-plane.
Constraint {
eventFirstPriority FALSE
inames [ "Card1" "Card1a" "Card2" "Card3" "Card4"]
inodes [ USE Card1, USE Card1a, USE Card2, USE Card3, USE Card4 ]
userFunctions [
"SFBool Collision(SFVec3f, SFVec3f, SFFloat)"
"function Collision (x1, x2, v) {
a=x1[0]-x2[0];
b=x1[1]-x2[1];
dst=a*a+b*b;
if (Math.sqrt(dst)< v ) return true;
return false;
}"
"SFBool Equal(SFVec3f, SFVec3f)"
"function Equal (x1, x2) {
if ( x1[0]==x2[0] && x1[1]==x2[1] && x1[2]==x2[2]) return true;
return false;
}"
]
constraints [
"Card1.translation=If (Collision(-3 -0.6 0, Card1.translation, 3),
If (Equal (Card1a.translation, -2.7 -0.6 0.4),
3 3 0,
-2.7 -0.6 0.4),
Card1.translation) "
"Card1.rotation=If (Collision(-3 -0.6 0, Card1.translation, 3),
1 0 0 1.5707,
0 0 0 0) "
"Card1a.translation=If (Collision(-3 -0.6 0, Card1a.translation, 3),
If (Equal (Card1.translation, -2.7 -0.6 0.4),
6 3 0,
-2.7 -0.6 0.4),
Card1a.translation) "
"Card1a.rotation=If (Collision(-3 -0.6 0, Card1a.translation, 3),
1 0 0 1.5707,
0 0 0 0) "
"Card2.translation=If (Collision(-3 -0.9 0, Card2.translation, 3),
-2.7 -0.9 0.4,
Card2.translation) "
"Card2.rotation=If (Collision(-3 -0.9 0, Card2.translation, 3),
1 0 0 1.5707,
0 0 0 0) "
"Card3.translation=If (Collision(-3 -1.2 0, Card3.translation, 3),
-2.7 -1.2 0.4,
Card3.translation) "
"Card3.rotation=If (Collision(-3 -1.2 0, Card3.translation, 3),
1 0 0 1.5707,
0 0 0 0) "
"Card4.translation= If (Collision(-3 -1.55 0, Card4.translation, 3),
-2.7 -1.55 0.4,
Card4.translation) "
"Card4.rotation=If (Collision(-3 -1.55 0, Card4.translation, 3),
1 0 0 1.5707,
0 0 0 0) "
]
}

Another example shows how a piece in a scene avoids collision with an obstacle represented by a tree. The constraint solver will change the position of the piece relative to its position. If the piece is moved in X-direction and it approaches the tree, the Z-position of the piece will be changed. After passing the tree, the old Z-position is restored and the piece moves along its original path.

birdx.translation = Follow (birdx.translation,
bird1.translation,..., birdx-1.tranlsation,
birdx+1.translation,..., birdn.tranlsation)
If an event occurs,
the function Follow computes the distances from the bird itself (first argument)
to all other birds. Then, the bird follows that bird with the smallest distance.

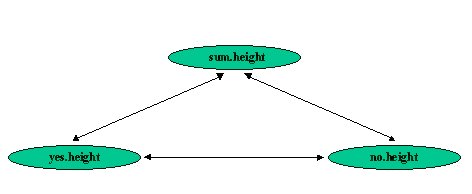
sum.height=yes.height + no.height yes.height=sum.height - no.height no.height=sum.height - yes.heightWith the help of our prototype this can be written as:
Constraint {
inames [ "SUM", "YES", "NO" ]
inodes [ USE SUM, USE YES, USE NO ]
constraints [
"NO.translation[1]=Sub (SUM.translation[1], YES.translation[1] )"
"YES.translation[1]=Sub (SUM.translation[1] , NO.translation[1] )"
"SUM.translation[1]=Add (YES.translation[1] , NO.translation[1] )"
]
}
Note, that these constraints are cyclic. As we
use local propagation which is unable to solve
cyclic constraints, we have to open the cycle
to guarantee termination of evaluation.
The result of the above constraints is, that whenever the
size of one cylinder is changed, e.g. by user interaction,
the size of the other two cylinders is adapted accordingly.

Constraint {
startEval TRUE
inames [ "WS" "NT" "Q" "SA" "NSW" "V" "T" ]
inodes [ USE WS_C USE NT_C USE Q_C USE SA_C USE NSW_C USE V_C USE T_C ]
constraints [
"WS.emissiveColor!=NT.emissiveColor"
"WS.emissiveColor!=SA.emissiveColor"
"NT.emissiveColor!=SA.emissiveColor"
"NT.emissiveColor!=Q.emissiveColor"
"SA.emissiveColor!=Q.emissiveColor"
"SA.emissiveColor!=NSW.emissiveColor"
"SA.emissiveColor!=V.emissiveColor"
"Q.emissiveColor!=NSW.emissiveColor"
"NSW.emissiveColor!=V.emissiveColor"
"V.emissiveColor!=T.emissiveColor"
]
domainDefs [
"MFColor M6 { 0 0 1 , 1 0 0 , 0 1 0 , 1 0 1 , 1 1 0 , 0 1 1 } "
"MFColor M4 { 0 0 1 , 1 0 0 , 0 1 0 , 1 0 1 } "
"MFColor M2 { 1 1 0 , 0 1 1 } "
]
domains [
"WS.emissiveColor=M6"
"NT.emissiveColor=M6"
"Q.emissiveColor=M4"
"SA.emissiveColor=M4"
"NSW.emissiveColor=M4"
"V.emissiveColor=M2"
"T.emissiveColor=M2"
]
}
The following image shows a map of australia, the height of each column
indicate the number of inhabitants in that part of the country. 

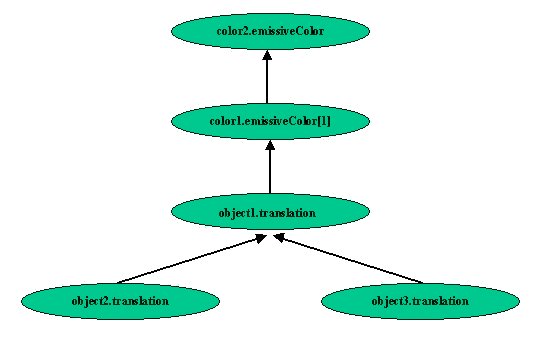
Constraint {
inames [ "object1" "object2" "color1" "color2 ]
inodes [ USE object1 USE object2 USE color1 USE color2 ]
constraints [
"object1.translation=Sub (object2.translation, object3.translation)"
"color1.emissiveColor[1]=Div (object1.translation[1], 10 ) "
"color2.emissiveColor=color1.emissiveColor[1] "
]
}
The following figure shows the dependency-graph of this example.
sum.height=yes.height+no.height yes.height=sum.height-no.height no.height=sum.height-yes.heightThe following figure shows the cyclic dependency-graph of this example.
By allowing the user to define own functions the constraints become more expressive and flexible. To implement this feature the constraint solver creates a new Script-node by the JS API-function createVRMLFromString(). For each function parameter an EventIn-Field will be created. To return the result, we simply use an EventOut. We also allow to use such a function several times in the constraints. Solving a constraint with a user function will be done in 3 Steps: First, all EventIn's are updated by setValue(). Then, the JavaScript-Function will compute the return-Value. Last, the constraintSolver gets the result by getValue(). These 3 steps efficiently allow the solver to use only one Script-node for a function but to use the function several times in the constraints.
| [Diehl:97a] | Stephan Diehl, VRML++: A Language for Object-Oriented Virtual Reality Models, In Proceedings of the 24th International Conference on Technology of Object-Oriented Languages and Systems TOOLS Asia'97, Bejing, China, 1997 |
| [Diehl:97b] | Stephan Diehl, Extending VRML by One-Way Equational Constraints, In Proceedings of the Workshop on Constraint Reasoning on the Internet, Linz, Austria, 1997 |
| [Diehl:98] | Stephan Diehl, Object-Oriented Animations with VRML++, In Proceedings of Virtual Environments Conference and 4th Eurographics Workshop, Stuttgart, Germany, 1998 |
| [Gobbetti&Balaguer:95] | Enrico Gobbetti,Jean-Francis Balaguer, An Integrated Environment to Visually Construct 3D Animations, In Proceedings of SIGGRAPH'95, 1995 |
| [Haridi_et_al:98] | Seif Haridi, Peter van Roy and Christian Schulter, Programming Languages for Distributed Applications, New Generation Computing, 3(16), 1998 |
| [Myers_et_al:96] | Brad A. Myers, Robert C. Miller, Rich McDaniel and Alan Ferrency, Easily Adding Animations to Interfaces Using Constraints, In Proceedings of the ACM Symposium on User Interface Software and Technology UIST'96, Seattle, WA, 1996 |
| [Richard:97] | Nadine Richard, Philippe Codognet, Multi-way Constraints for Describing High-Level Object Behaviours in VRML, In Proceedings of the Workshop on VRML and Object Orientation, Monterey, 1997 |
| [Reynolds:87] | Craig W. Rainolds Flocks, Herds and Schools: A distributed Behaviour Model in Symlouics Graphics Division, Los Angeles 1987 |
| [Sutherland:69] | I. Sutherland, Sketchpad: A man-machine graphical communication system, In Proceedings of the IFIP Spring Joint Computer Conference, 1963 |
| [Zanden_et_al:94] | Brad Vander Zanden, Brad A. Myers, Dario Guise and Pedro Szekely, Integrating Pointer Variables into One-Way Constraint Models, In ACM Transactions on Computer Human Interaction, Vol. 1, 161-213, 1994 |